Machine Learning: Classification
Announcements
- Assignment 7: Due Wednesday May 18th
- Grades are up for assignment #6
- Please take a few minutes to complete a course eval
- You should have received an email from
StudentCourseEvaluations@umbc.eduwith a link to the surveys for classes in which you are enrolled - Deadline is May 17th
- You should have received an email from
Let's recap regression.
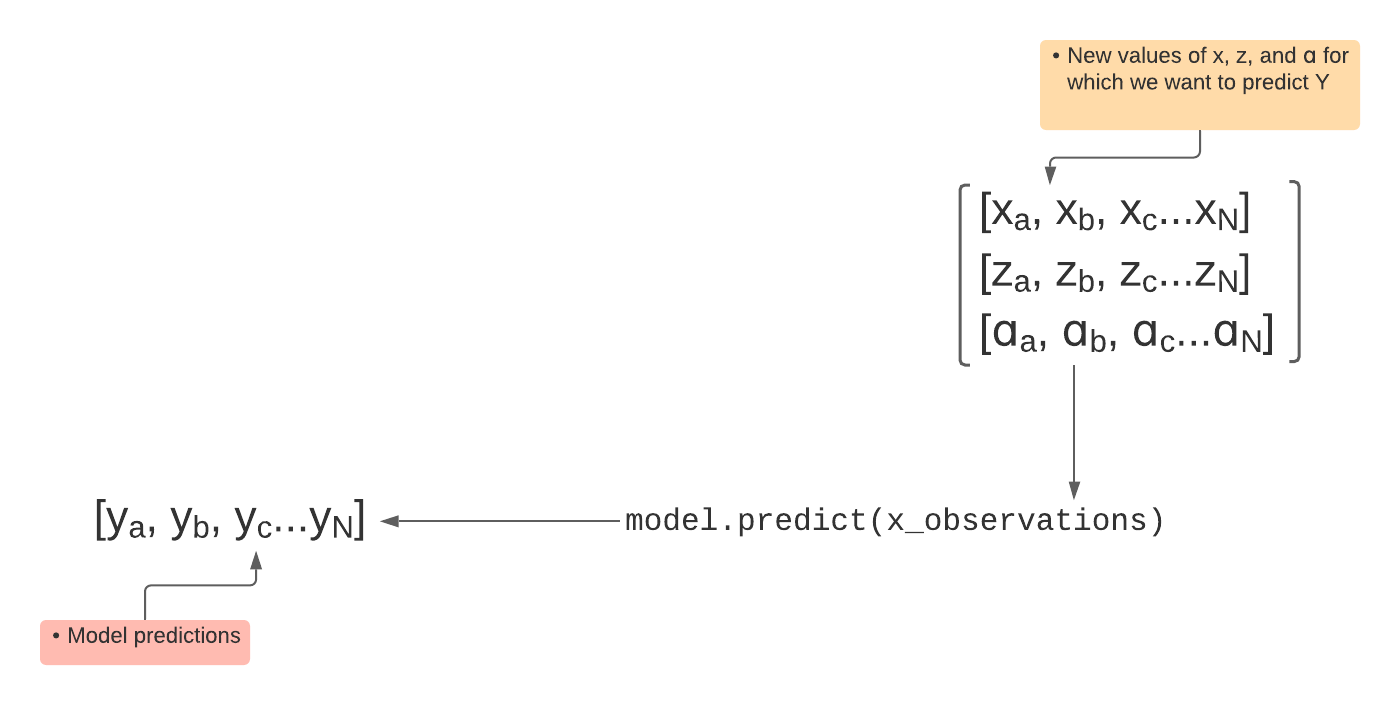
Input Data: univariate regression

Model training
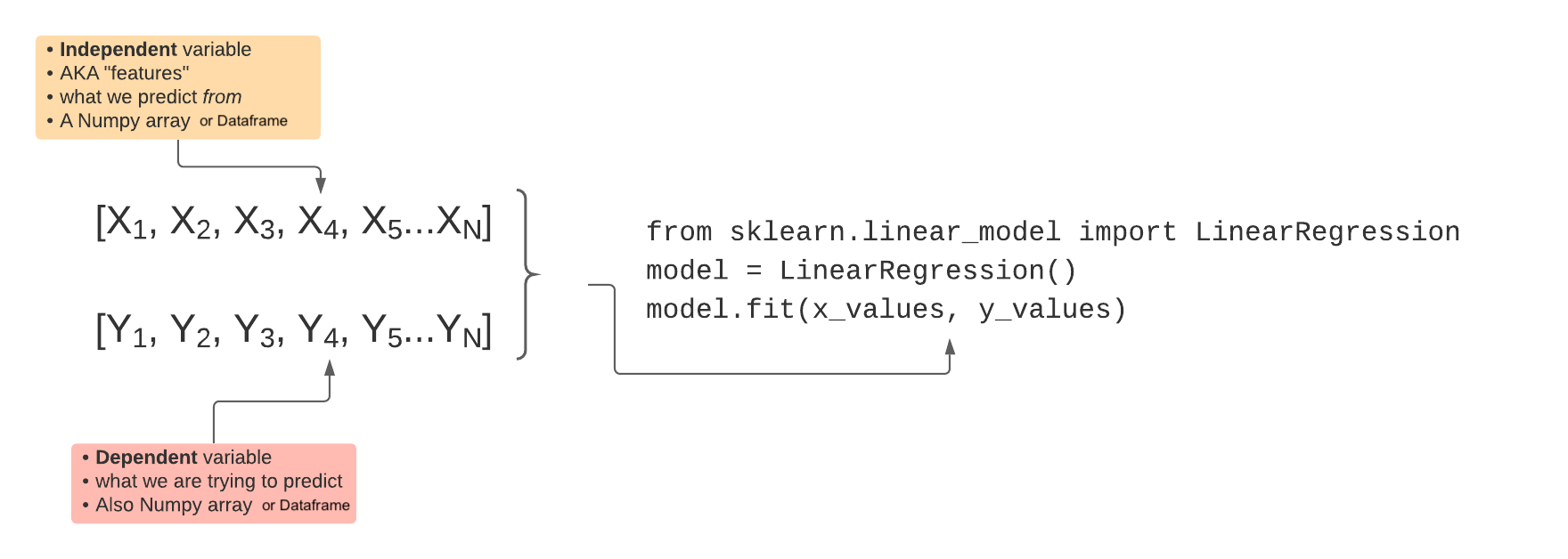
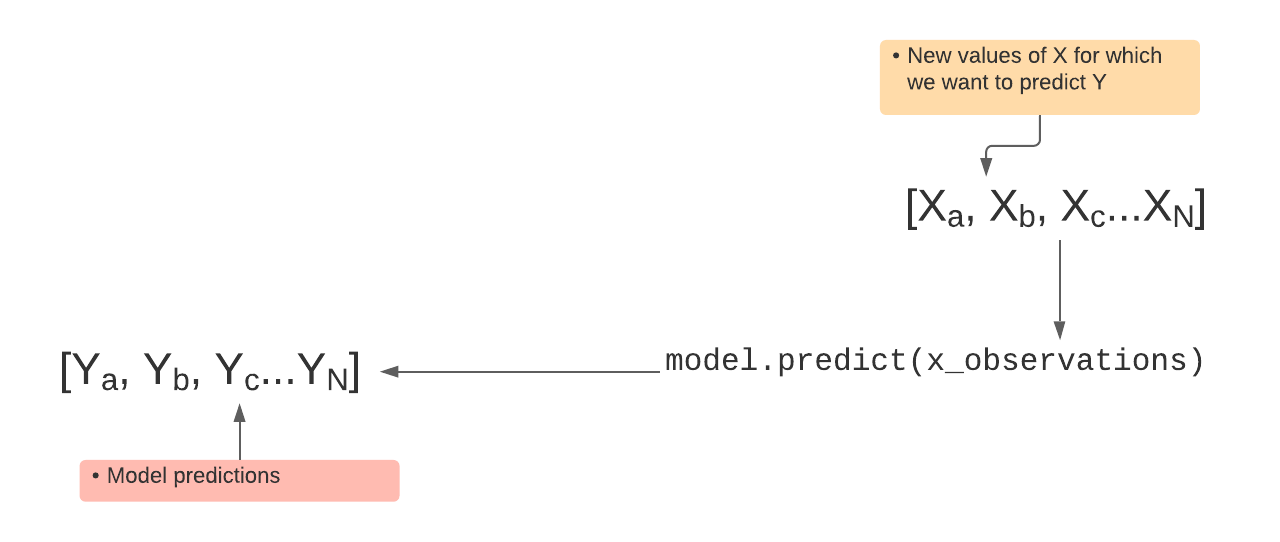
Predicting with the model
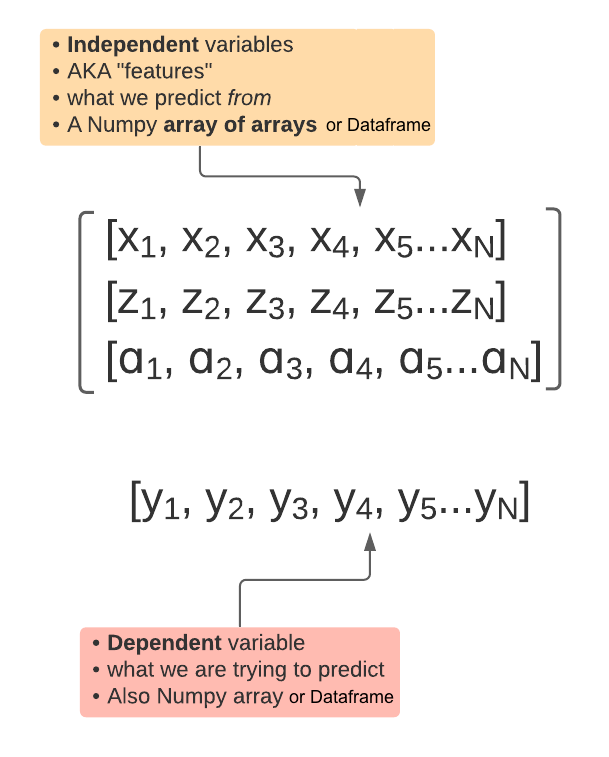
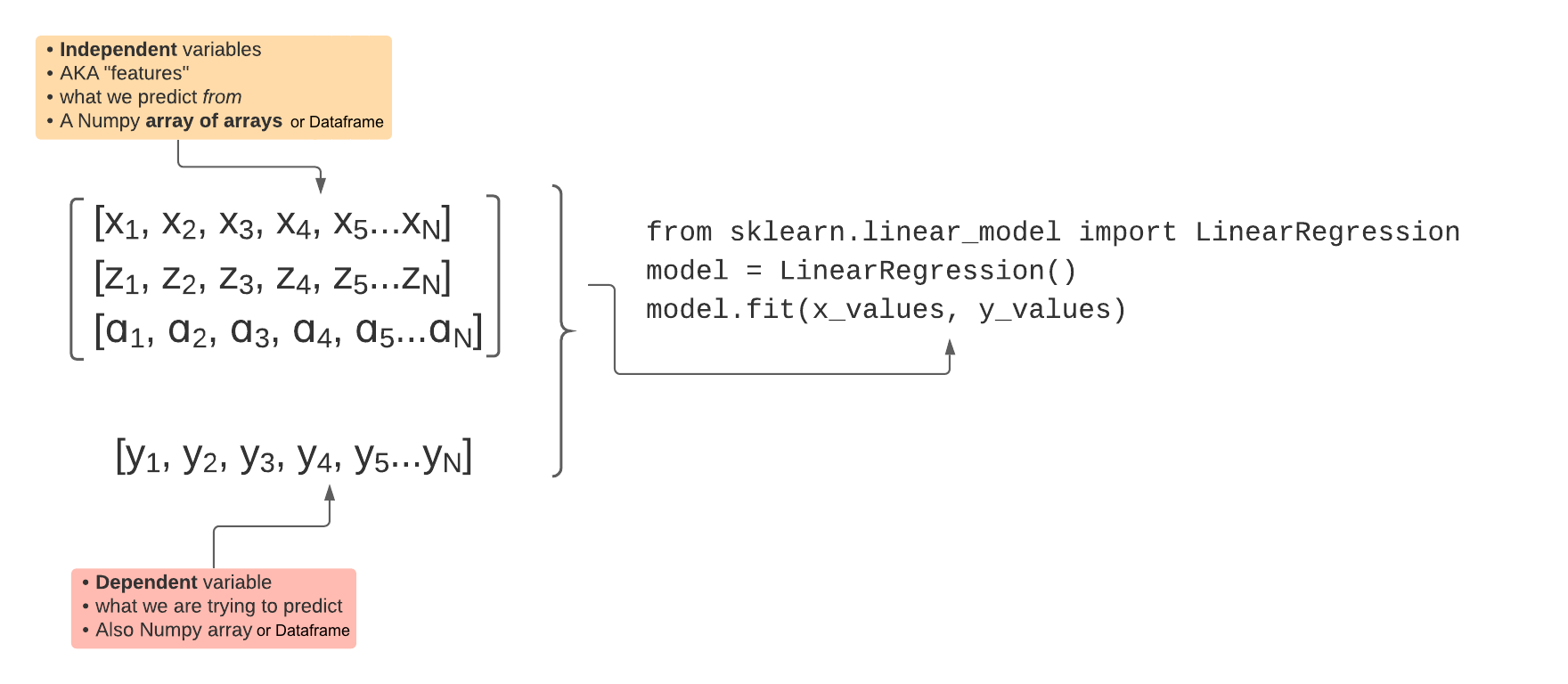
Input Data: multivariate regression
Model training
Predicting with the model
Let's talk about classifiers...
- Regression is about finding a function that models the relationship between features and predictor
- Classification is about finding a function gives us a decision boundary
Naive Bayesian Classifier

Thomas Bayes
What makes the Naive Bayes Classifier Good?
- Simple
- Intuitive
- Works surprisingly well
How does it work?
- Let's say we have three categories: 1, 2, and 3
- And we have a bunch of features,
X =[x1,x2,x3...xn] - Every
xbelongs to one of three categories: 1, 2, or 3 - We want to calculate probability. Given a single x, what is the probability of it's being a y?
- Which value of y has the highest probability? That's the one we choose to classify our x as.
- But how do we do that?
Enter Bayes' theorem
\[\begin{aligned} P(Y|X) = \frac{P(X|Y)P(Y)}{P(X)} \end{aligned} \]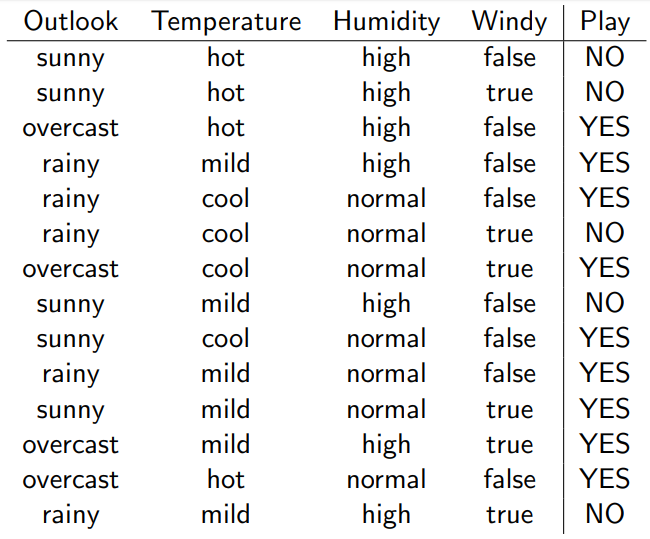
We can calculate P(Y)
\[\begin{aligned}
P(Y\equiv Play) = \frac{\#Play}{\#Play + \#NoPlay}
\end{aligned} \]
We can calculate P(X)
\[\begin{aligned}
P(X\equiv Sunny) = \frac{\#Sunny}{\#Sunny + \#Overcast + \#Rainy}
\end{aligned} \]
We can calculate P(X|Y)
\[\begin{aligned}
P(X \equiv Sunny|Y\equiv Play) = \frac{\#Play \& \#Sunny}{\#Play}
\end{aligned} \]
The problem is that this gets huge
- For a model with k binary features, there are: \[\begin{aligned} 2^{k+1} \end{aligned} \] ...parameters to calculate
- 8 parameters are needed for a 2-feature binary dataset
- To get around this we pretend all features are independent
- This is the "naive" part of the algorithm. Parameters to calculate now: \[\begin{aligned} 2k \end{aligned} \]
k-Nearest Neighbors
A lazy learner
- How do we chose a value for
k? - This is called a hyperparameter
- If
kis too low, noise will have higher influence on the result. Overrfitting - High value for
kis expensive to compute - Use the elbow method