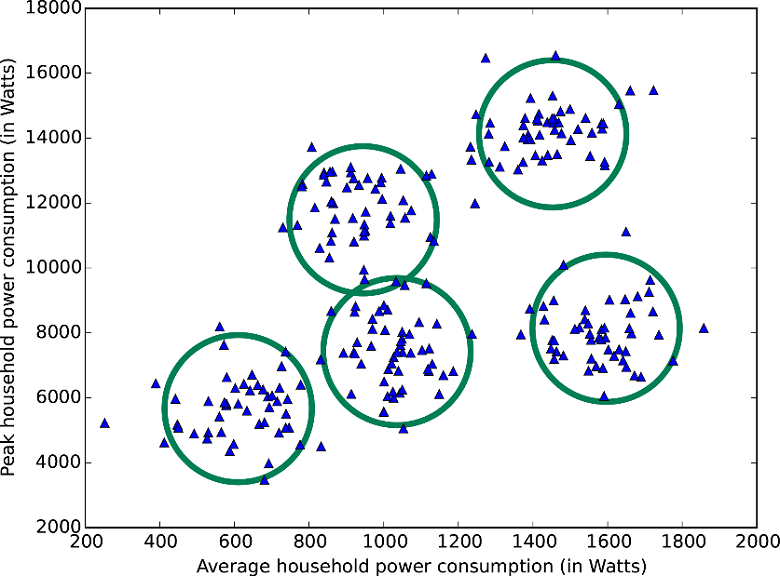
Machine Learning
Introduction
This is a huge topic
So how do people learn?
- We gain information through observation or instruction
- We apply this information to tasks
- We generalize this information to related domains
"Machine Learning" is—obviously—far more simplistic.
"A computer program is said to learn from experience E with respect to some class of tasks T and performance
measure P, if its performance at tasks in T, as measured by P, improves with experience E."
—Tom Mitchell,
Professor of Machine Learning, CMU
Professor of Machine Learning, CMU
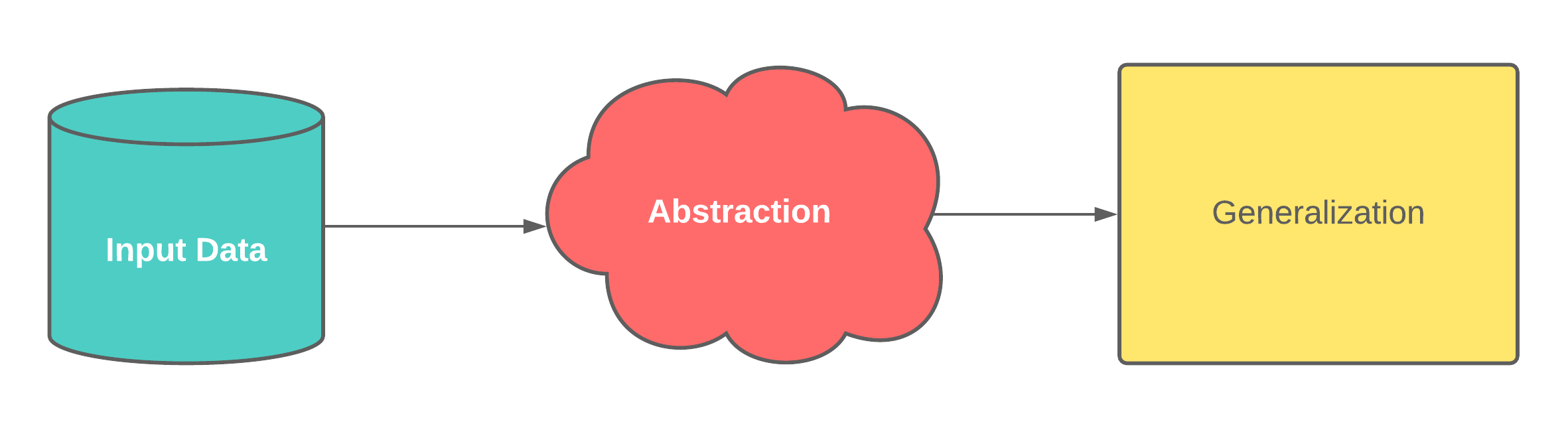
Input Data
- Features: individual measurable property or characteristic of a phenomenon being observed
- Numeric data
- Labeled images, documents, or audio
- Graphs/Relationships
Abstraction
- Features are used to derive a model
- A model is a summarized/generalized knowledge representation of the input data
- Computational blocks (like if/else rules)
- Math equations
- Data structures like trees and graphs
- Logical groupings of similar features
Abstraction, Cont'd
Different problems require different modeling approaches:
- Characterize the relationship between features
- Predict some value given other information
- Classify a thing by category
- Group similar things together
Generalization
- Apply the model to new data
- Evaluate the performance of the model
- Make improvements
- Try again
- A model generalizes well when we can apply it to new data and it gives us the right answers
None of this is magic.
- You need quality input data
- You need to be able to formulate a problem in a way that ML can work with
- You may need to spend time creating data to learn from
- You will need to spend time evaluating the result
Remember this?
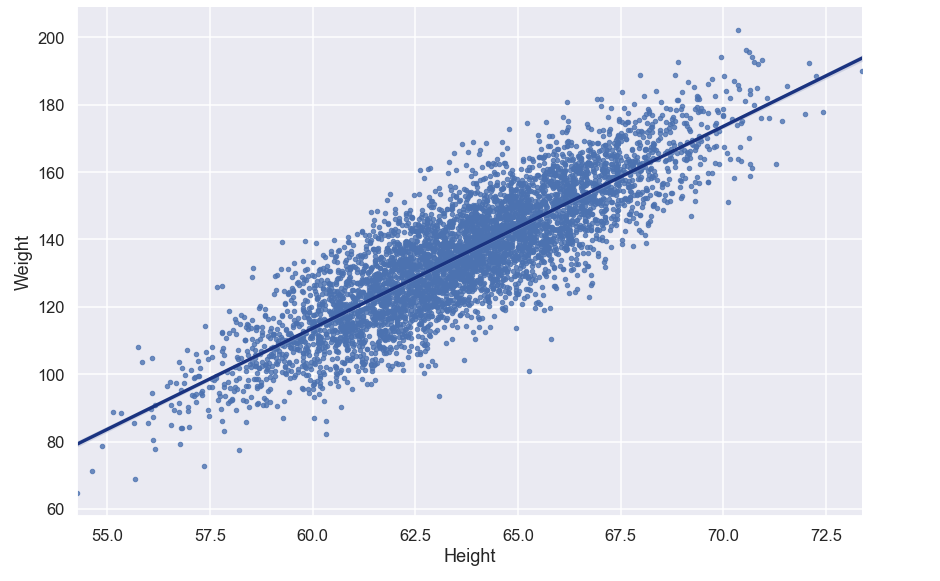
(Lecture 10: Exploratory Data Analysis)

- Input data: height and width measurements
- Abstraction: we have a prediction problem
- "Given their height, can we predict someone's weight?"
- Output is a math equation:
y = mx + b - Our model learns the value of
mandb
- Generalization: test with real data. How well does it predict?
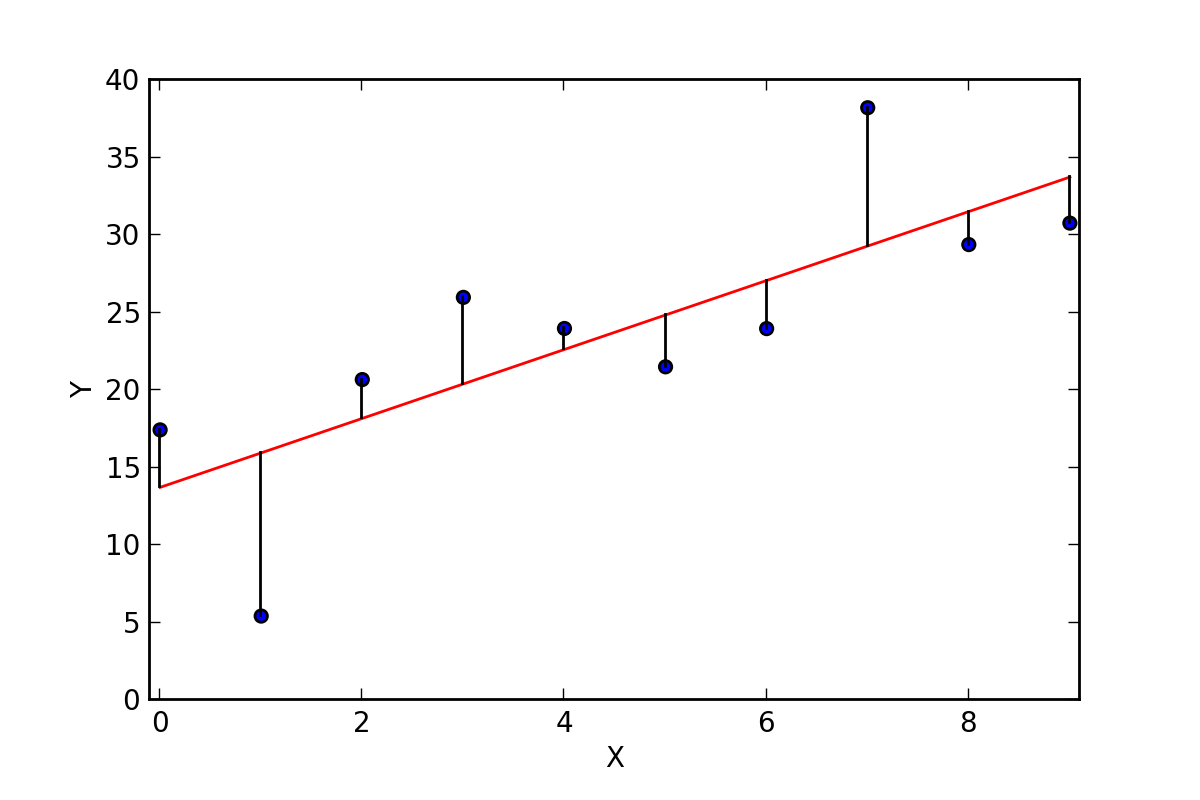
- We can formulate this problem (and a lot of ML problems) as trying to minimize a loss function
- How much does our model miss the target?
- Keep adjusting until our model is as close as it can be.
Mean Squared Error (MSE)
 \[\begin{aligned}
MSE = \frac{1}{n}\sum_{i=1}^{n} ({Y_{i} - \hat{Y_{i}}})^2
\end{aligned} \]
\[\begin{aligned}
MSE = \frac{1}{n}\sum_{i=1}^{n} ({Y_{i} - \hat{Y_{i}}})^2
\end{aligned} \]
Mean Squared Error (MSE)

total = 0
for point in points:
err = distance(point, line)
total += (err * err)
MSE = total / len(points)
MSE is not the only loss function.
- There are many
- Some work better than others depending on:
- Kind of data
- Kind of ML task
- How you want penalize (or weight) certain kinds of error
- Mean absolute error (MAE) - doesn't penalize large errors
- Likelihood Loss: good for comparing different models
- Hinge Loss: good for classification
There is a solution that will find the slope (m) and y-intercept (b) of a line that minimizes MSE. It is called Ordinary least squares (OLS) regression
\[\begin{aligned} m = \frac{\sum_{(x_{i} - \overline{x})(y_{i} - \overline{y})}}{\sum_(x_{i} - \overline{x})^2} \\ b = \overline{y} - m * \overline{x} \\ \end{aligned} \]- OLS is easy because it is a closed-form solution
- You have a formula, you plug in the values, you get an answer
- It is also very fast to compute (with you have a univariate solution)
- It only useful for linear regression
- What if we have a multivariate problem? (e.g. age, and height to predict weight)
- What if the solution is non-linear?
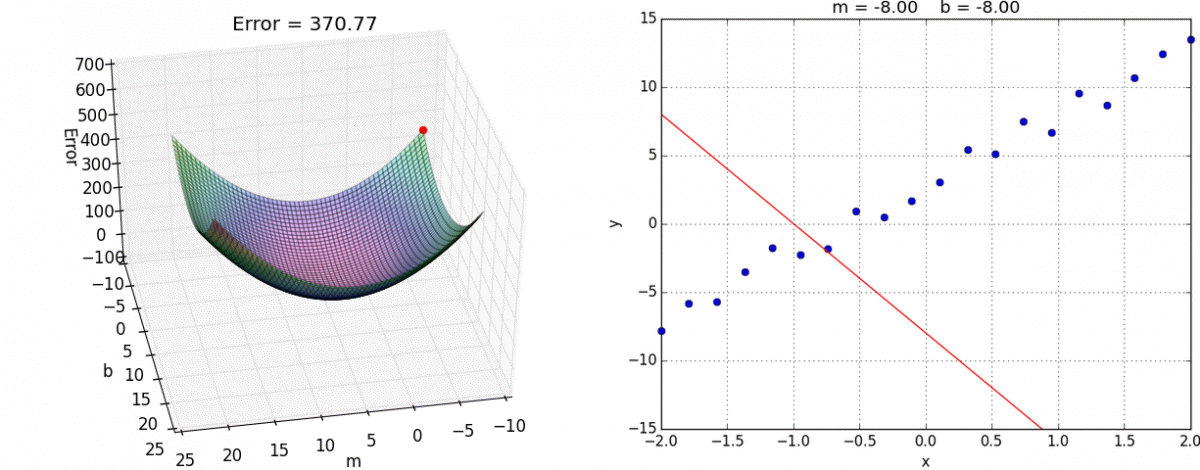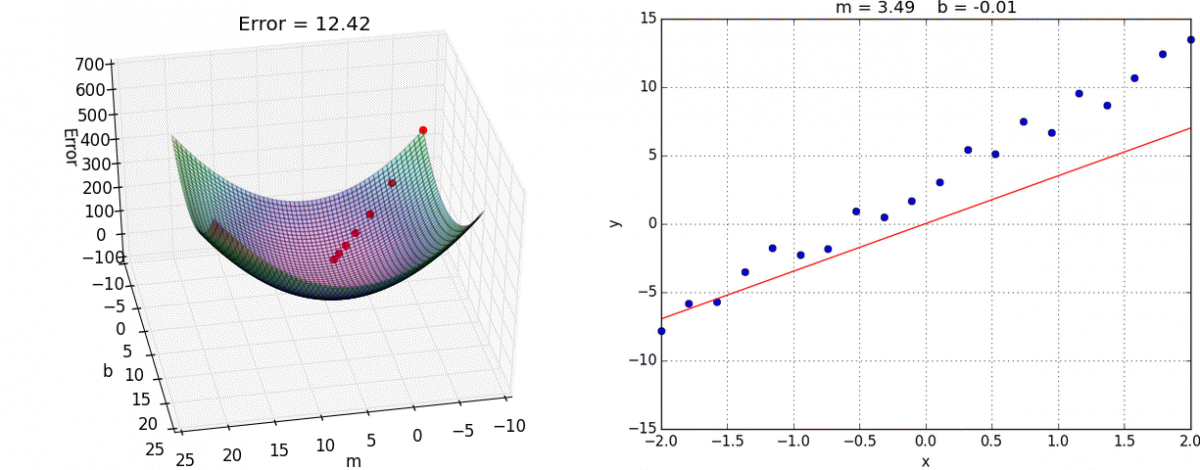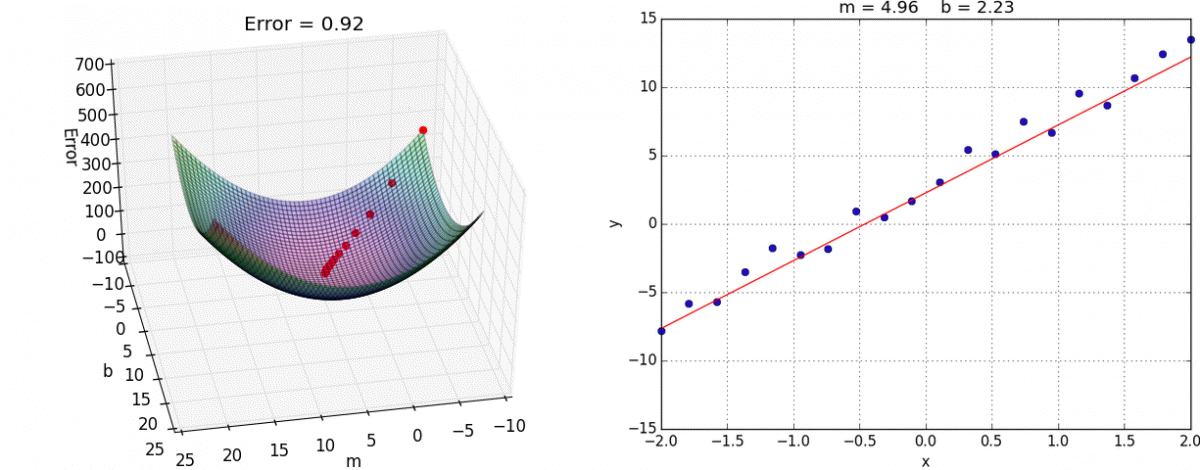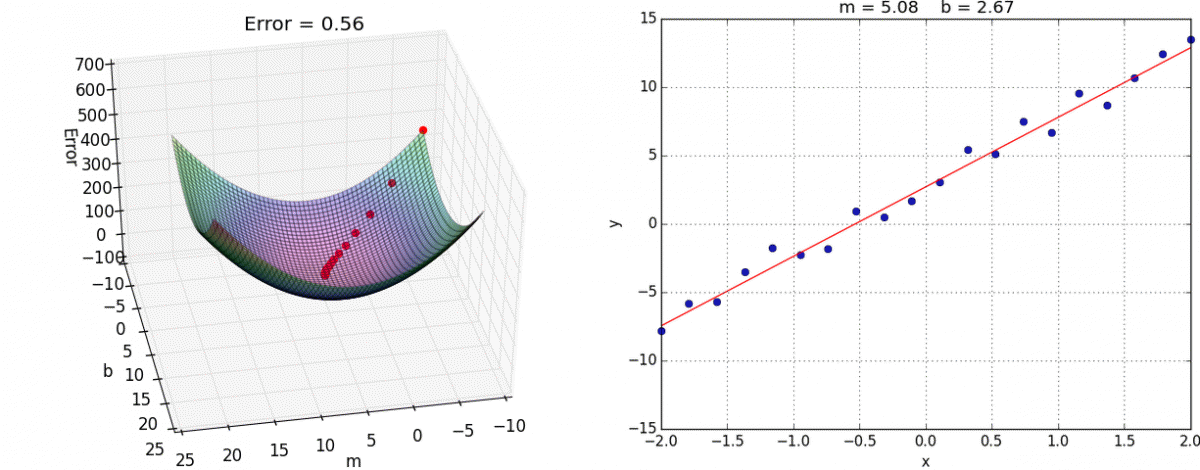
Gradient Descent
Another (more general method) to minimize a loss function like MSE
- Faster to compute with multivariate regression
- Can minimize loss function for non-linear solutions too
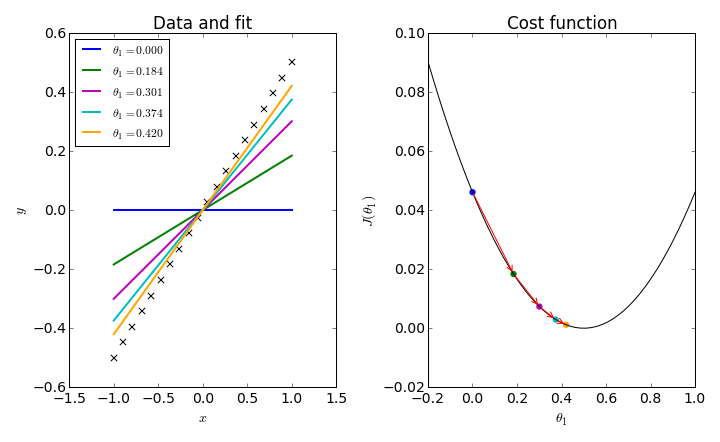
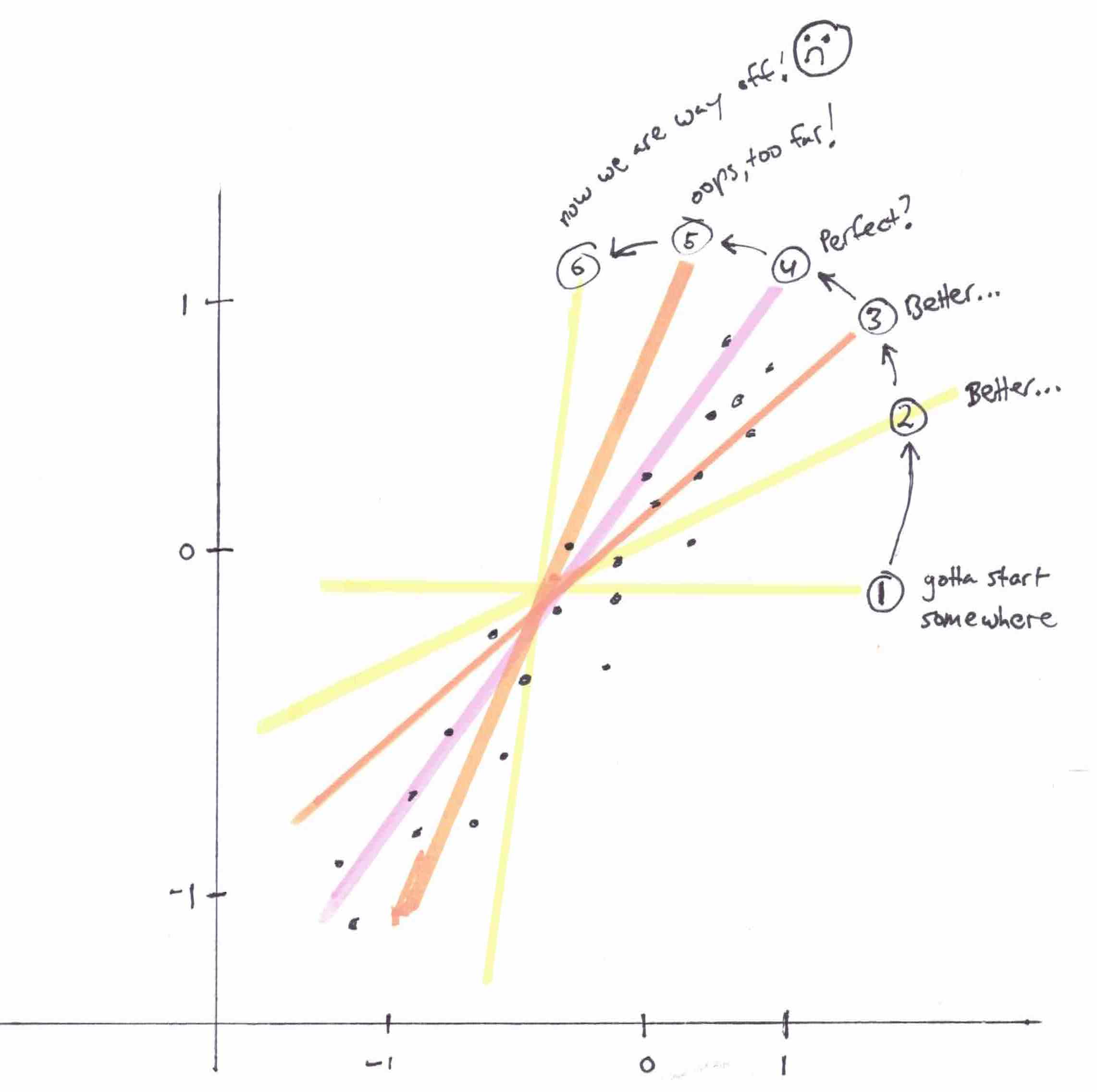

When the slope is zero, we know we have minimized our loss function
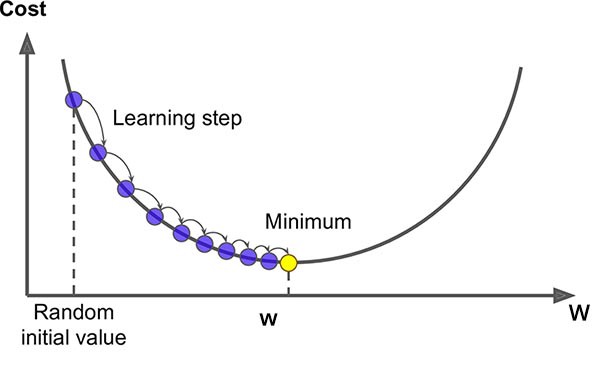
As we get closer, our steps get smaller and smaller
There are two main categories of machine learning algorithms
- Supervised Learning
- Unsupervised Learning
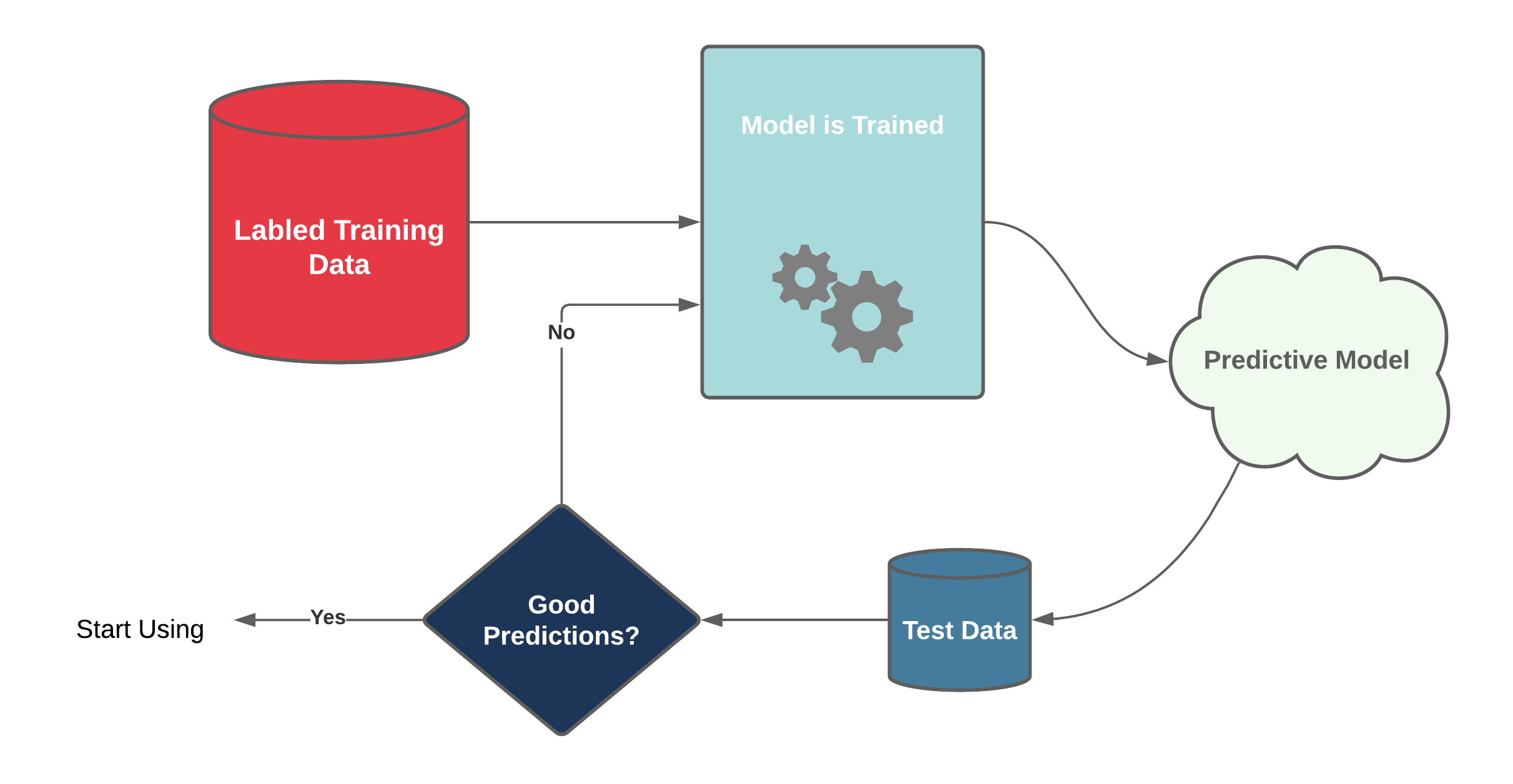
Supervised Learning
- Algorithms that "learn" from past information
- Needs training data
- Linear regression in an example
- We gave it training data (height/width measurements)
- It learned to predict height based of width from this data
Supervised Learning Tasks
- Prediction (AKA regression)
- What is our forecasted earnings growth?
- What is the likelihood it will rain?
- What is the most effective dosage for this patient?
- We are predicting continuous values
- Classification
- Image classification
- Handwriting recognition
- Is this email spam or not? (binary)
- We are predicting discrete values
Bad training data makes bad models
Unsupervised Learning
- No labelled training data to learn from, no prediction to be made
- Primarily about looking for patterns in data
- Can we group things together?
- Are there hidden relationships among things?
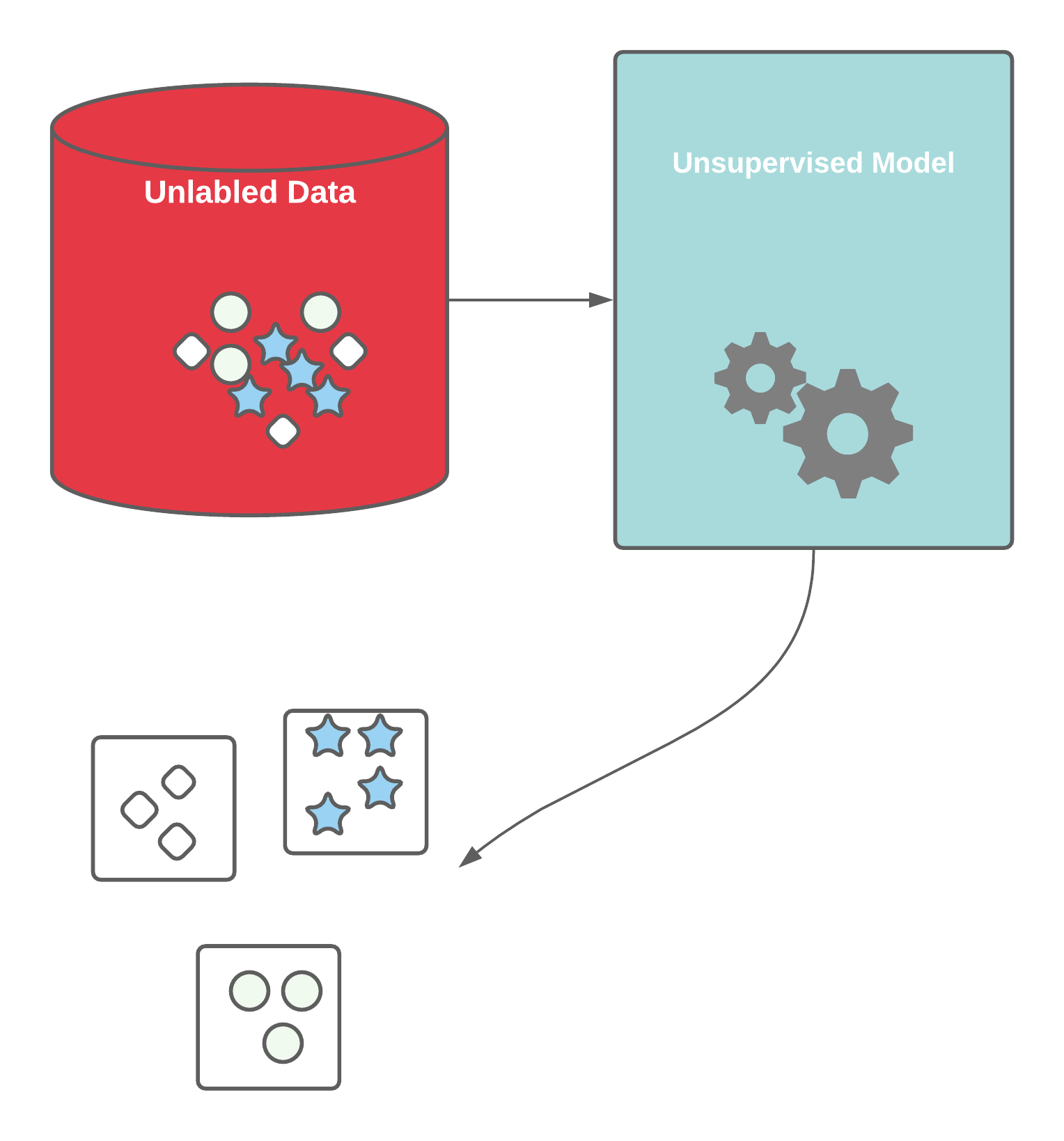
Clustering
- Group or organize similar objects together
- Can we draw boundaries around objects in N-dimensional space?